中心性算法用于理解图中特定节点的左右及其对网络的影响, 可以帮助我们识别最重要的节点.

本文将介绍以下算法:

• 度中心性算法: 可作为连通度的基准指标.
• 紧密中心性算法: 用于度量节点在群组中的中心程度.
• 中间中心性算法: 用于寻找图中的控制点.

度中心性 Degree Centrality

用于度量节点拥有的关系数量, 数值越大表示其中心性越高.

• 输入: G = (V, E).
• 输出: 每个节点及其度中心性值.

实现原理

$$C'_D(N_i) = \frac{N_{degree}}{n - 1}$$

其中:

• $N_{degree}$ 表示节点的度.
• $n$ 表示节点数量.

该公式已标准化.

对于异质图的适配

• 该指标计算不涉及属性, 只关注图结构的度.
• 只计算同 label 下的度.

紧密中心性 Closeness Centrality

用于发现可通过子图高效传播信息的节点, 数值越高表示其与其他各个节点的举例最短. 当需要知道哪个节点的传播速度最快的时候可以使用该算法.

• 输入: G = (V, E).
• 输出: 每个节点及其紧密中心性.

实现原理

衡量节点中心性的指标是其到其他各个节点的平均距离. 紧密中心性算法在计算所有节点对之间的最短路径的基础上, 还要计算它到其他各个节点的距离之和, 然后对结果求倒数.

$$C(u) = \frac{1}{\sum_{v=1}^{n-1}d(u,v)}$$

其中:

• $u$ 表示节点.
• $n$ 表示图中节点数量.
• $d(u,v)$ 表示另一个节点 $v$ 和 节点 $u$ 之间的最短距离.

更常见的作法是将计算结果进行归一化, 以此表示最短路径的平均长度, 而不是最短路径之和. 归一化公式如下:

$$C_{norm}(u) = \frac{n-1}{\sum_{v=1}^{n-1}d(u,v)}$$

对于异质图的适配

• 只计算同 label 之间的节点.

• 实际上只计算每个连通子图中的紧密中心性.

  Wasserman & Faust 算法

  该算法是针对于非连通图的变式.

  $$C_{WF}(u) = \frac{n-1}{N-1}\left(\frac{n-1}{\sum_{v=1}^{n-1}d(u,v)} \right)$$

  其中:

  • $u$ 表示节点.
  • $N$ 表示总的节点数量.
  • $n$ 表示与 $u$ 在同一个分量中的节点的数量.
  • $d(u, v)$ 表示另一个节点 $v$ 到 $u$ 的最短距离.

中介中心性 Betweenness Centrality

用于检测节点对图中信息流或资源的影响程度, 通常用于查找将图的一部分与另一部分桥接的节点.

• 输入: G = (V, E).
• 输出: 每个节点及其中介中心值.

实现原理

$$B(u) = \sum_{s \neq u \neq t} \frac{p(u)}{p}$$

其中:

• $u$ 表示节点.
• $p$ 表示节点 $s$ 和 $t$ 之间最短路径的总和.
• $p(u)$ 表示 $s$ 和 $t$ 之间通过节点 $u$ 的最短路径的数量.

下图中展示了计算中介中间性得分的步骤.

中介中心性计算示例

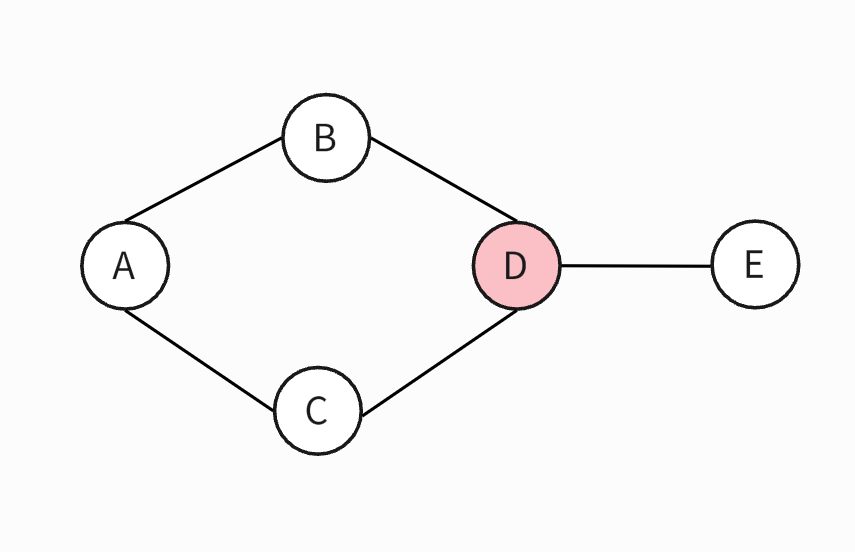
针对节点 D 的计算过程如下:

通过 D 的最短路径节点对	节点对之间的最短路径总数 $p$	占通过 D 最短路径数量的百分比 $\frac{p(u)}{p}$
(A, E)	1	1
(B, E)	1	1
(C, E)	1	1
(B, C)	2 (分别是 B->A->C 和 B->D->C)	0.5

所以根据公式, 节点 D 的中介性得分是: 1 + 1 + 1 + 0.3 = 3.5.

对于异质图的适配

• 该指标计算不涉及属性, 只关注图结构的度.
• 只计算同 label 下的度.

本文参考资料

1. 《数据分析之图算法：基于Spark和Neo4j》

贡献者

• liuyanliang

版权所有

版权归属：liuyanliang

本文链接：/article/dsg3yb5o/

许可证：署名-非商业性-禁止演绎 4.0 国际 (CC-BY-NC-ND-4.0)